 Magnetospheric
electric fields
Magnetospheric
electric fields Magnetospheric
electric fields
Magnetospheric
electric fieldsspaceweb@oulu.fi - last update: 23 November 1998, 2000 UT (RR)
The are two main sources of magnetospheric electric fields. The other is the solar wind related, dawn-to-dusk directed ("convection") field, and the other is the co-rotation electric field related to the rotation of the Earth along its spin axis. The electric fields have a strong effect on the drift paths of the magnetospheric plasma. The low energy particles move primarily under the E×B drift, and are less affected by the gradient and curvature drifts which depend only on magnetic field. The energetic particles, following the magnetic drifts more readily, are also affected by the convection field. See also solar wind - magnetosphere - ionosphere coupling.
In the open magnetosphere model initially suggested by Dungey (1961), reconnection (or merging) of the interplanetary and geomagnetic field lines partially opens Earth´s magnetic field to the solar wind. For this to happen, the field lines must be oppositely directed: a southward interplanetary magnetic field (IMF) is thus needed to open Earth's closed dayside magnetic fields. The antisunward magnetospheric convection is produced when the reconnected, open field lines are swept over the polar caps at the solar wind speed. The dawn-to-dusk solar wind electric field E = vsw × Bsw maps along the field lines, and an antisunward E×B drift of plasma is formed also in the polar cap F-region ionosphere. When the northern and southern hemispheric field lines are streched into a magnetic tail by the solar wind, they eventually reconnect with each other deep in the untisunward region. This magnetic geometry has a tension that exerts a force on the plasma. Together with the pressure gradient and the potential difference applied across the magnetosphere by the flowing solar wind, these forces produce motion of the magnetospheric plasma on closed field lines towards the Sun, and an associated dawn- to-dusk magnetospheric electric field in the tail. The mapping of this electric field into the ionosphere produce a dusk-to-dawn electric field and sunward plasma flow in the auroral zone: the familiar two-cell pattern of ionospheric convection is formed. If the southward IMF periods continues for several hours, the magnetosphere reaches a steady-state like configuration called steady magnetospheric convection, SMC.
The magnetospheric potential and electric fields can be approximated by using the Volland's potential distribution (Volland, 1973) and the multiplier A according to Maynard and Chen (1975):
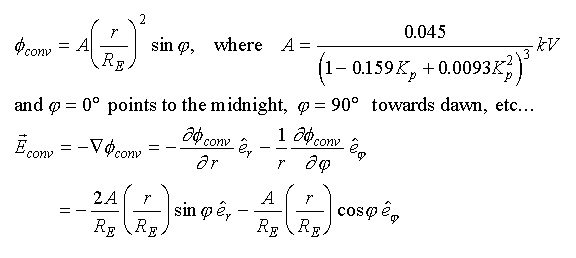
Note that A = A(Kp), and that it raises fastly from A = 45 V at Kp = 0 to over 800 V at Kp = 6. The model is thus recognizing the fact that the convection electric field increases during magnetically active times.
This equatorial field can be used only with equatorially mirroring particles. For off-equatorial particles, one must always trace the field lines to the equator to get the potential from the above equations in three points so that the vector field can be calculated at the given points (Ondoh and Aikyo, 1986; Cladis and Francis, 1989).
Note that when the plasma flows toward Earth because of the convection field, a zonal charge separation opposing the field is created as electrons drift dawnward and protons duskward around the Earth. The inner magnetosphere is thus shielded from the magnetospheric electric field, and the electric field due to the rotation of the Earth is dominating. Inside this region, called the plasmasphere, cool dense plasma is flowing in concentric circles around the Earth.
We will first derive an approximation for the co-rotational electric field in the equatorial plane. This can be done by using the simple dipole model for B, B=B0/r^3, and equating the created Erot×B drift with the speed of the co-rotating plasma. Note that this produces azimuthally symmetric field. Integrating the electric field equation we get a very simple equations for the electric field and its potential:
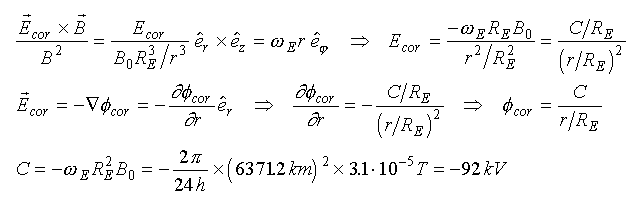
A better way would be to calculate the potential at the surface of the Earth, C cos²L, where L is the geomagnetic latitude, and map to the region of interest along magnetic field lines using realistic field models. This way the calculated field will not be azimuthally symmetric, and you can follow also the off-equatorial particle drift.
See also: