(5) Maps of the HeavensCoordinates on a Flat Plane
Back in the 1600s, a French scientist, Rene Descartes ("De-cart"), devised a systematic way of labeling each point on a flat plane by a pair of numbers. You may well be already familiar with it. The system is based on two straight lines ("axes"), perpendicular to each other, each of them marked with the distances from the point where they meet ("origin")--distances to the right of the origin and above it, the origin being taken as positive and on the other sides as negative (see drawing below). 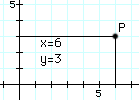
The distance on one axis is named "x" and on the other axis "y". Given then a point P, one draws from it lines parallel to the axes, and the values of x and y at their intersections completely define the point. In honor of Descartes, this way of labeling points is known as a cartesian system and the two numbers (x,y) that define the position of any point are its cartesian coordinates. Graphs use this system, as do maps. The two representations are closely related. From the definitions of the sine and cosine x = r cos f That allows (x,y) to be derived from polar coordinates. To go in the opposite direction and derive (r,f) from (x,y), note that from the above equations (or from the theorem of Pythagoras) one can derive r: r2 = x2 + y2 Once r is known, the rest is easy cos f = x/ sr These relations fail only at the origin, where x = y = r = 0. At that point, f is undefined and one can choose for it whatever one pleases. Coordinates in Three Dimensions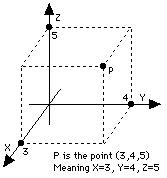
Up to here numbers were used to specify points on a flat plane, for instance a sheet of paper. The real world, however, is 3-dimensional, and sometimes it is necessary to label points in 3-dimensional space. The cartesian (x,y) labeling can be extended to 3 dimensions by adding a third coordinate z. If (x,y) is a point on the sheet, then the point (x,y,z) in space is reached by moving to (x,y) and then rising a distance z above the paper (points below it have negative z). Very simple and clear, once a decision is made on which side of the sheet z is positive. By common agreement the positive branches of the (x,y, z) axes, in that order, follow the thumb and the first two fingers of the right hand when extended in a way that they make the largest angles with each other. Again, the cartesian labeling (x,y,z) is nicely symmetric. Sometimes, though, it is convenient to follow the style of polar coordinates and label distance and and direction separately. Distance is easy: you take the line OP from the origin to the point and measure its length. You can even show from the theorem of Pythagoras that in this case r2 = x2 + y2 + z2 But what about direction? Azimuth and Elevation
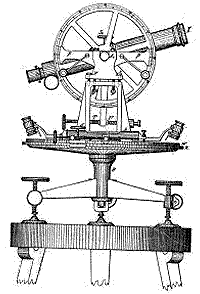
Look again at the surveyor's telescope: the direction to which it points is completely specified by two angles--its azimuth f, the angle by which its base is rotated on a horizontal table-- and its elevation l (small Greek L), the angle by which it is lifted above the horizontal (if it looks down, l is negative). The two angles together can in principle specify any direction: f ranges from 0 to 3600, and l from -900 (straight down or "nadir") to +900 (straight up or "zenith"). Again, one needs to decide from what direction is the azimuth measured--that is, where is azimuth zero? The rotation of the heavens (and the fact most humanity lives north of the equator) suggests (for surveyor-type measurements) the northward direction, and this is indeed the usual zero point. The azimuth angle (viewed from the north) is measured counterclockwise. [A note to the mathematically inclined. One would think that the 3-dimensional generalization of polar coordinates would use (r,l,f) to label any point in space. Mathematicians however prefer their own notation and replace l, measured from the horizontal, with q = 90 - l deg. which is the angle between OP and the vertical and goes from 0 to 1800, not from -900 to + 900. This may actually make more sense, because it is easier to measure an angle between two lines (OP and the vertical) rather than between a line and a flat plane (OP and the horizontal).] Right Ascension and DeclinationIn mapping the positions of stars in the sky, direction is all one can readily measure, and a system similar to (l,f) is used. But while in the surveyor's telescope the preferred direction (the one around which azimuth is measured) is the vertical one, in the sky the preferred axis is obviously the one pointing to the north pole of the heavens. In place of azimuth and elevation, the two angles are now named right ascension (RA) and declination, and are denoted by the Greek letters a (alpha) and d (delta). In the equatorial mounting of telescopes a ring around one axis shows the declination at which the telescope is pointing and one around the other axis the right ascension. The First Point in Aries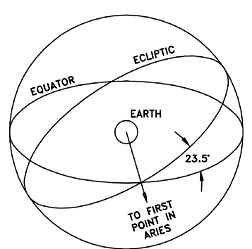
Given the system of celestial coordinates it is now possible to measure the declination and right ascension of stars, and to draw maps showing their positions and the constellations which they form. One problem here is that one cannot map the surface of a sphere onto flat paper without distortion: the same problem arises in mapping the surface of the Earth, and map-makers have long ago devised a variety of mapping methods, each with its advantages and drawbacks. This matter is sidestepped here by assuming the heavens to be mapped onto a globe, and in fact such globes do exist. The star chart now resembles the celestial sphere, with the difference that instead of being at the center looking out, we are on the outside looking in. Polaris will be very near the north pole, and the equator will be halfway between the poles--for instance, the constellation of Orion straddles it and one of the 3 stars in Orion's "belt" is practically on top of it. And the ecliptic, equally long, cuts the equator at an angle of 23.5 degrees (see drawing) Yet one essential detail is still missing. Just as azimuth is measured from the northward direction, right ascension must have a zero mark somewhere. And it does: by common agreement, it is one of the points at which the ecliptic cuts the equator, the one occupied by the Sun in spring. Since that point is on the ecliptic, it is expected to belong to one of the constellations of the zodiac. Two thousand years ago or so, when the positions of stars were first measured, it was in the constellation of Aries, the ram. Over the centuries, it has slowly migrated (as is discussed in the next section) to the neighboring constellation of Pisces, the fish. However the old name is still used, the "first point in Aries," though some also refer to it as the "spring equinox" or "vernal equinox." |

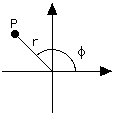 But there also exist other ways of labeling a point P on a flat plane by a pair of numbers, ways which can be more useful in special situations. One way ("polar coordinates") uses the length r of the line OP from the origin to P (i. e. the distance of P distance to the origin) and the angle that line makes with the x-axis. Angles are often denoted by Greek letters, and here we follow conventions by marking it with f (Greek f). Note that while in the cartesian system x and y play very similar roles, here roles are divided: r gives distance and f direction.
But there also exist other ways of labeling a point P on a flat plane by a pair of numbers, ways which can be more useful in special situations. One way ("polar coordinates") uses the length r of the line OP from the origin to P (i. e. the distance of P distance to the origin) and the angle that line makes with the x-axis. Angles are often denoted by Greek letters, and here we follow conventions by marking it with f (Greek f). Note that while in the cartesian system x and y play very similar roles, here roles are divided: r gives distance and f direction.