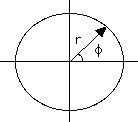
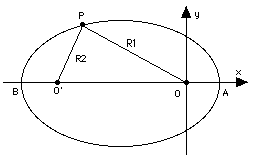
The ellipse has many interesting properties. It is a symmetrical figure and a second focus O' can also be drawn. Furthermore, it can also be defined (the original definition, in fact) as the collection of points for which the sum R1+R2 of their distances from two fixed points is always the same, and those points are the foci (Latin plural) O and O'.
The longest dimension of the ellipse, its width AB along the line connecting the two foci, is its "major axis." Suppose (R1,R2) are the distances of A from the foci O and O'. Then R1 = OA = a(1 - e) is the smallest distance of the ellipse from O, R2 = O'A = OB (by symmetry) is the largest and therefore equals a(1 + e). But, OA + OB = AB, hence
AB = a(1 - e) + a(1 + e) = 2a
Hence the quantity a in the equation of the ellipse is known as semi-major axis. We can now state Kepler's law more precisely as "the square of the orbital period T is proportional to the cube of the semi-major axis of its orbit around the Sun."
The two quantities (a,e) completely define the ellipse. When that ellipse is the orbit of a planet or a satellite, they form two of the six orbital elements which define the state of the orbiting body. A third element, the mean anomaly, specifies the position of the planet or satellite along the orbit, and the remaining three define the orientation of the orbit in 3-dimensional space. More about the orbital elements can be found in section (12a)
Refining the First Law
Kepler's first law was:
"The orbit of a planet is an ellipse, with the Sun at one focus"
Actually, this is not 100% accurate. Imagine the planet magically getting heavier and heavier, while the Sun is getting lighter and lighter. At some point both of them would be equally heavy: could we then say which is orbiting around which?
To be fully accurate, the first law should have placed the focus of the orbital ellipse at the center of gravity of the planet-Sun system. (The center of gravity will be defined later, but intuitively, if the masses are very unequal, as with a planet and the Sun, it lies close to the center of the heavier object.) Because the Sun is so much heavier than the Mars, the effect on the orbit of Mars (which Kepler studied) was too small to be noted by him. Nevertheless, the Sun also moves in response to motions of its planets, and motions of this type have become an important tool in the search for planets outside the solar system.
An Earth-sized planet orbiting a distant star would be far too dim to be seen with any earthly telescope, especially against the glare of its sun, the star itself. However, as the planet goes around the orbit, its star also moves in a mirror image orbit around the common center of gravity. It is a much smaller orbit and a much slower motion, because the center of gravity is very close to the center of that star (in the Earth-Sun system, it is inside the Sun), but it can still be detected by subtle variations of the starlight. Recently a few such planets have been found, but most are Jupiter-sized and none seems suitable for life. The search, however, goes on.
Bodies in the solar system can also move in other conic sections, in parabolas or hyperbolas, whose equations resemble that of an ellipse, but have e equal to 1 or larger. Such bodies are not bound to the Sun, but are free to escape it. The denominator in the equation of the trajectory
r = a(1 - e2)/ (1 + e cos f)
then becomes zero for some values of f, making r infinite, and as the moving body approaches those values, that body moves further and further away, with no limit. Comets in general have and eccentricity e close to 1, suggesting they have come from the very distant fringes of the solar system. The space probe Voyager 2 has e > 1 and is on its way out of the solar system, never to return.