(18) Newton's Second Law
For more money bills with famous physicists, click here
The second law gives an explicit formula, and hence is the one most useful. But it can also be the one that physics students find most confusing. Their problem may be stated as follows:
Good question. Generations of physics students have struggled with it, and all too often, so did their teachers. Some fell back to defining mass by weight, using gravity as a tool. One teacher I know, a distinguished physicist, brandished his arm in front of the class and defined force by analogy with what was produced by his muscles. Mach's formulation of Newton's laws
Ernest Mach, who lived in Germany two centuries after Newton, gave what may be the most satisfactory answer. Mach argued that Newton's laws boil down to one law:
Read it again, if you will: no mention of force or mass, only of acceleration, which can be measured. When a gun acts on a bullet, a rocket on its exhaust jet, the Sun on Earth (and on the scale of the distance separating the two, Sun and Earth can be viewed as compact objects), the accelerations are always oppositely directed. Mass and force are now readily derived. If one of the objects is a liter of water, its mass is defined as one kilogram. If it then acts on another object (perhaps with the water frozen into ice, for the purpose of the experiment), then the ratio of its acceleration aw to the acceleration of the other object gives the object's mass m: aw/a = m /1 kg = m Then m a = 1 kg. aw This can be interpreted to say that a force of magnitude aw units exists between the two F = m a = 1 kg. aw This unit of force would be the force causing 1 kg to accelerate at 1 meter/sec2--that is, its velocity increases each second by 1 meter/sec. It seems only fitting that such a unit is named the newton. After all, Newton was the one who, by that formula, made all motions amenable to calculations, and engineers everywhere apply it every day to practical purposes. No wonder that the poet Alexander Pope, who lived in Newton's time, wrote:
GravityOh yes, gravity. A falling body has the same acceleration g -- about 10 meter/sec2 --whether it is light or heavy. Where does F = ma enter here? Newton named the force which produces the fall gravitation, and he proposed that it was proportional to mass. Measured in newtons, with m in kilograms, that force is F = m g Putting this in the formula F = m agives m g = m a or a = g The last line shows that the acceleration of a falling object always equals g, whether it is a pebble or a big rock. The force pulling the rock down--its "weight"--is much bigger: however its mass, the inertia which must be overcome to move it, is bigger too, by the same factor. The upshot is that, big or small, the acceleration always equals g. That was what had confused scientists before Newton. When heavy and light stones were observed to fall at the same rate, the role of mass was not at all clear.
We are into some pretty deep waters here. The mass of an object can obviously be measured in two different ways (that is, compared to the mass of one liter of water). One can use gravity, weigh it, and get the gravitational mass--let's denote it m. Or one might dispense with gravity, like the astronauts aboard Skylab--and measure the "inertial mass", say M. One can visualize a universe where the two are different, but our own universe does not seem to behave that way. The Hungarian physicist Roland Eötvös (Lorand in Hungary) compared the two around the turn of the century, using extremely sensitive instruments, and concluded that they were the same to an accuracy of many decimals. That equality has become one of the foundations of physics, especially of the general theory of relativity. Objects at RestWhen you stand on the floor, gravity still pulls your body down with a force F = +mg (downwards) 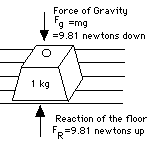
Why then don't you fall? Because the floor will not let you! Its component particles stick together and don't allow your feet to go down any more (the way they might if you were standing on quicksand). The fact the force F produces no acceleration is evidence that another force, opposing the motion, is produced by the floor: F' = -mg (upwards) Together, F and F' add up to zero, and the result is that your feet and your body stay at rest. That is a general rule: if nothing moves, the forces must add up to zero. They are then said to be "in equilibrium," a notion which will be found useful in the next section. Note this has nothing to do with Newton's 3rd law: the 3rd law deals with forces that produce motion, while here the forces all cancel.
|




