 | | Table of Contents | Introduction | Matrix of Transformation | Attitude Data Files | Software | Data Availibility | Additional Information | |  |

|
Every set of attitude coefficients (corresponding to a line in attitude data file) is valid for its own time interval and gives the possibility to get a matrix N of tranformation from the GSE coordinate system to the S/C coordinate system as well as a matrix M of tranformation from the S/C coordinate system to the GSE coordinate system.
Every set consists of 20 parameters. There are:
1. Line number
2. Year
3. Month
4. Day
5. Beginning of the time interval (in thousands of sec)
6. Interval duration (in thousands of sec)
Parameters 7-20 are attitude coefficients:
7-11. A1 - A5
12-16. B1 - B5
17. ω1
18. ω2
19. c1
20. c2
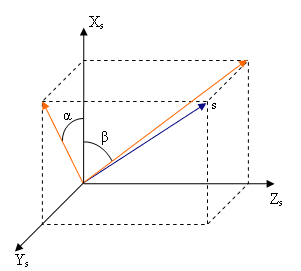
Using the coefficients we can get angles α, β, γ:
 |
 |
α is an angle between XS axis and the Sun projection onto XSYS plane,
β is an angle between XS axis and the Sun projection onto XSZS plane.
The algorithm is based on the assumption that the α,β angles can be approximated by the following functions:
α = A1 +
A2sin ω1 t +
A3cos ω1 t +
A4sin ω2 t +
A5cos ω2 t,
β = A1 +
B2sin ω1 t +
B3cos ω1 t +
B4sin ω2 t +
B5cos ω2 t.
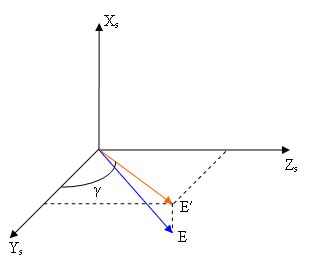
γ is an angle between YS axis and projection of the North Pole of Ecliptic onto XSYS plane.
As this direction is close to the one which is orthogonal to the spin axis the linear approximation of the γ angle is valid:
γ = c1 + c2 t
ω1 is the spin rate of the Sun direction around the angular momentum vector;
ω2 is the spin rate of the the angular momentum vector around the main axis of inertia XS.
Using α, β angles the Sun direction (which coincides with XG axis) cosines in the S/C coordinate system can be calculated:
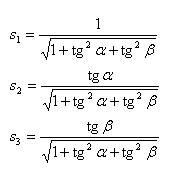
The direction e of the North Pole of Ecliptic plane (which coincides with ZG axis cosines in the S/C coordinate system can be calculated by formulas:
ax = s2 cos γ + s3 sin γ
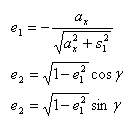
So we have the direction cosines of XG and ZG axis in the S/C coordinate system.
The third direction p is
and the matrix M of transformation from the S/C to the GSE systems (the direction cosines matrix) is:
| M = |
|
and the matrix N of transformation from the GSE system to the S/C system is the transpose of matrix M:
| N = |
|
Any vector VS/C in the S/C coordinate system can be transformed to the GSE coordinate system using M matrix:
as well as
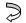
|
Back to INTERBALL home page |