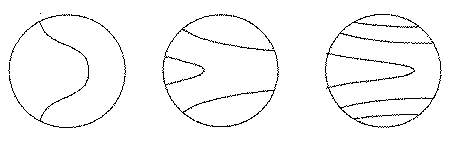|
12. Sunspots
The story of the Earth's magnetism is strongly tied to that of solar research, in several ways. Large magnetic storms, and observations of "northern lights" far south from their usual locations (i.e. of the "aurora borealis," now commonly known as "polar aurora"), were found to be associated with solar phenomena. And not only did the Sun have a magnetic field, but concentrated sources of that field--dark sunspots--were visible on its surface, quite unlike the sources of the Earth's field which are buried deep in the Earth's core. This led to valuable insights into how the geomagnetic field might be generated. Sunspots were first reported in 1609, independently by Galileo, Scheiner and Fabricius [Newton, 1958; Phillips, 1992], all of whom used the newly invented telescope. Sporadic reports of earlier observations also exist, because the unaided eye can see large sunspots when thick haze dims the Sun near the horizon. Unfortunately, sunspots practically disappeared for a 70-year period starting around 1645 ("the Maunder minimum"). During those years the interest of astronomers wandered elsewhere, and when spots again became frequent, they were not investigated systematically. The 11-year sunspot cycle was discovered accidentally by Heinrich Schwabe (1789-1875), a German pharmacist and amateur astronomer living in the town of Dessau [Meadows, 1970; Newton, 1958]. Schwabe was looking for a yet-unknown planet of the Sun, moving inside the orbit of Mercury. Such a planet (given by other searchers the tentative name of Vulcan) would be hard to spot (except during a total solar eclipse) because its position in the sky would always be close to that of the Sun, where daylight would obscure it. Schwabe hoped to observe it as a dark spot moving across the face of the Sun, and day after day, year after year, whenever the sky was clear, he observed the Sun and looked for it. To properly conduct such a search, Schwabe also had to identify and track sunspots, to make sure none was mistaken for a new planet. He did so from 1826 onwards, and by 1843 he noted a cyclical rise and fall in their number, as well as in the number of days when no spots were observed. He then published a table of his yearly totals, but until 1851 it attracted little notice, except from Rudolf Wolf, noted below. Then Alexander von Humboldt republished it (extended to 1850) in the third volume of his "Kosmos," and suddenly sunspots and their cyclic behavior became a hot scientific topic. Rudolf Wolf (1816-93) of Berne (later of Zürich) collected earlier observations, tracing sunspot cycles before Schwabe's time. He introduced the "Zürich sunspot number," an empirical criterion for the number of spots, taking into account the fact they usually occurred in tight groups. The length of the sunspot cycle turned out to vary, but the average value was near 11 years. Sir Edward Sabine (1852) found an association between the sunspot cycle and the occurrence of large magnetic storms, and Richard Carrington (1826-75), also in England, studied the rotation of sunspots around the Sun, noting that their period and other properties depended on latitude. In September 1859 Carrington (as well as R. Hodgson, another British observer) saw by chance a bright outburst of light in a group of large sunspots, lasting about five minutes [Meadows, 1970; Newton, 1958]. This was followed 17 hours later by a very powerful magnetic storm, strongly suggesting a connection, although Carrington cautiously commented "One swallow does not make a summer." But what were the sunspots themselves? We now believe that they appear darker because they are slightly cooler than the regions that surround them. Galileo speculated that they might be clouds floating in the Sun's atmosphere, blocking some of its light. Their most significant feature, however, was discovered only in 1908, by George Ellery Hale (1868-1938), leader among US astronomers, founder of great observatories and designer of novel instruments [Wright, 1966]. One of his inventions (in 1892) was the spectroheliograph, also devised independently in France by Deslandres (1853-1948), a spectrograph adapted to scan the Sun in a single spectral color, producing a photographic image. Whereas in white light the Sun presented (apart from its spots) a bland appearance, the spectroheliograph (e.g. tuned to the red H_ line of hydrogen) isolated light from higher layers in the Sun's atmosphere and revealed many new features. These included mottling of the surfaces, prominences arching high above the Sun (turning to dark linear features when passing in front of the Sun) and bright areas near sunspots. Hale also found that "solar flares," such as the one observed by Carrington and Hodgson, were much more frequently seen in H__light, and big ones indeed often preceded magnetic storms. In 1896 Pieter Zeeman discovered the "Zeeman effect" by which the characteristic colors ("spectral lines") of elements, when emitted by a gas located in a strong magnetic field, often split into two or more components of slightly different wavelength, with their separation depending on the intensity of the field. Using the Zeeman effect, Hale in 1908 showed that sunspots were in fact strongly magnetic, with a typical field intensity of 1500 gauss (0.15 Tesla). The spots generally appeared in pairs of opposite polarity, suggesting that field lines emerged from the Sun at one of the pair and re-entered at the other. One spot was usually ahead of the other in the direction in which the Sun rotated, and the magnetic polarity of the "leading" spot north of the equator, in any solar cycle, was always the same, and was opposite to the "leading" polarity south of the equator. In the following solar cycle both these polarities were always reversed, suggesting that the sunspot cycle was a magnetic phenomenon, with an average period near 22 years.
Hale's method was greatly refined by Horace Babcock [Babcock, 1960, 1963; Phillips, 1992; Eddy, 1978], Robert Leighton and others. Using the polarization of Zeeman lines to construct a "solar magnetograph," they greatly increased the sensitivity of Hale's method, to the point where not only sunspot fields could be observed, but also a general dipole field of the Sun, of the order of 5 gauss. The existence of such a field had been suspected from a feature of the solar corona, the Sun's outer atmosphere, previously seen only during total eclipses of the Sun. At the poles the corona displayed rays or "plumes" in a pattern which reminded observers of magnetic field lines of a dipole, like the ones above the poles in Figure 6. The magnetograph also showed that this field reversed each 11-year solar cycle, typically 3 years after sunspot minimum.
13. The Dynamo Process on the Sun
The Sun is a giant ball of gas, hot enough to conduct electricity (i.e. a plasma), much hotter than anything that exhibits permanent magnetism. Sunspot magnetism therefore had to come from electric currents, and in 1919 Sir Joseph Larmor proposed that such currents could be produced by a self-sustaining fluid dynamo [Larmor, 1919]. A Faraday disk can serve as a model of such a dynamo, if its magnetic field is created by an electromagnet, powered by the output current of the same disk (other types of generator also can be so designed). Energy must be supplied by the outside force which rotates the disk., and the presence of iron is not essential: if the "electromagnet" has an iron-free core, the magnetic field produced in it may be much weaker, but it would still exist.
But what comes first in a dynamo, the magnetic field needed for producing the current, or the electric current needed to produce the field? This sounds a bit like asking, what came first, chicken or egg? Actually, if conditions are appropriate, even a very weak initial field is amplified exponentially, rising until (neglecting friction, viscosity, acceleration etc.) the opposing magnetic force on the current creates a torque matching the applied one.
Larmor suggested that a similar situation may arise in an electrically conducting fluid, in which suitable flows are produced, e.g. circulation of the fluid due to heat convection, that can play the role of a rotating disk. He was quite tentative about it--just one brief paragraph, followed by two alternative suggestions (and his follow-up note of 1927 did not get any closer). The idea survived in part because nothing else seemed to lead anywhere, but implementing it--finding such flows in a conducting medium--proved quite difficult. In a conventional dynamo, the electric current is channeled by wires wrapped in insulators, in a way forcing it to generate the required magnetic field. In a continuous conducting fluid, no such channeling exists.
Attempts to model fluid dynamos were further discouraged by the "anti-dynamo" theorem of Thomas G. Cowling (1906-1990), who proved that the fluid dynamo problem had no axially symmetric solutions [Cowling, 1933, 1985]. That eliminated easy and simple solutions, and some researchers began to wonder whether solutions existed at all.
A useful concept in the theory of plasmas and of conducting fluids is the "freezing" of magnetic field lines, developed by Walén [1946] and by Alfvén [1950; Alfvén and Fälthammar, 1963] , although the idea itself may be older. It can be shown that in a fluid with extremely high electrical conductivity, such field lines are "frozen" into the plasma, in the sense that two particles which share the same field line at any time, usually continue doing so later on, even when the flow has separated them and has deformed their magnetic field. In fluids whose conductivity is merely large, not infinite, Cowling showed that field lines slowly slipped from their "frozen" positions. The criterion for "extremely high" also involved the dimensions of the flow, and was therefore more likely to be fulfilled by large-scale flows, on the Sun and in the Earth's core, rather than in the laboratory.
For instance, the "solar wind" which flows more-or-less radially outwards from the Sun is a hot plasma and may be viewed as such a conductor. The region at which this wind originates is permeated by magnetic fields, originating in the global solar dipole and in sunspot regions. As some solar wind ions move out radially to the Earth's orbit and beyond, others on the same field lines but deeper in the Sun's atmosphere stay behind. By the "field line preservation" theorem, however, they continue to share the same field line.
Out near Earth, the field carried by the first group forms the local interplanetary magnetic field (IMF). The particles left behind on the Sun, on the other hand, have meanwhile rotated with the Sun to other meridians. Solar wind particles on the same field line will therefore be on different meridians than the "roots" of that line on the Sun. The longer these particles have traveled through space, the more have their "roots" rotated and therefore the greater the difference in solar longitude from those roots, suggesting that the magnetic field lines curve to form a spiral, which ultimately becomes wrapped tighter and tighter. This curvature has indeed been observed by spacecraft, at the Earth's orbit and throughout the solar system, suggesting that the solar wind "remembers" its solar roots for days and even months after leaving the Sun.
The stretching of magnetic field lines in general implies an amplification of the magnetic field. The intensity of the IMF, for instance, decreases with distance R from the Sun like R-1
(for the azimuthal component, in the direction of the rotation) or like R-2
(for the other components), whereas that of the undistorted dipole decreases much faster, like R-3
. If the Sun's field were a pure dipole, its intensity at the Earth's orbit would be much weaker than what is actually observed.
On the Sun, such stretching may be expected from the observed uneven ("differential") rotation of the photosphere, the visible surface layer of the Sun. The rotation period, as seen from Earth (whose motion around the Sun adds to it about 2 days) can be measured from the apparent motion of sunspots, and its value in days, as function of the latitude in degrees, is shown in Table 1 [Newton, 1958]
|