#12d   La distance D entre les trajectoires de Venus

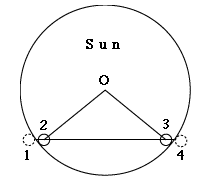
    Les éphémérides concernant le passage donnent quatre temps de "contact", relatifs à la façon dont le disque sombre de Venus tangente le bord du disque du soleil (marqué par des chiffres sur la Figure 3)"

   
Premier contact : le disque de Venus touche le soleil par l'extérieur, en y entrant
Second contact : le disque de Venus touche le soleil par l'intérieur, en y entrant.
Troisième contact : le disque de Venus touche le soleil par l'intérieur, sur la sortie
Quatrième contact -- le disque de Venus touche le soleil par l'extérieur, sur la sortie

Fig. 3   les 4 contacts de Venus et le disque du soleil

    Venus n'est évidemment pas visible lors des 1ers et 4èmes contacts, et nous n'utiliserons donc que le 2ème contact (pour définir A ou A ')et le 3ème contact (pour définir B ou B ') (voir la figure).

    Le disque du soleil présente un diamètre apparent 2R d'environ 31.5 minutes d'arc, tandis que le rayon r de Venus est d'environ 1 minute. Comme déjà dit à propos de AB etc. à la page précédente, R et r ne sont pas des distances mais des angles apparents. Mais dans ce calcul tous les angles peuvent toujours être maniés comme des distances, parce qu'ils sont très petits. Vous pouvez imaginer le schéma 3 projeté à l'intérieur d'une énorme sphère (par exemple le dôme d'un planétarium, ou celui de la sphère céleste elle-même). Un secteur d'une moitié de degré, soit le diamètre approximatif du soleil, couvre une si petite partie de la sphère entière qu'avec une bonne approximation on peut le considérer comme plat, et les distances qui y sont mesurées sont pratiquement proportionnelles aux angles auxquels ils correspondent.

    Nous situons les points A et B non pas au bord ("limbe") du disque du soleil lors des 2ème et 3ème contact, mais au centre de Venus correspondant à ces heures. Si O est le centre du soleil, ces points se trouvent sur un cercle de centre O avec un rayon (R–r). Ainsi le temps du trajet AB lors du passage de Venus correspond à la corde (=coupant le cercle directement en droite ligne) d'un "soleil réduit" à seulement 30.5 minutes d'arc.

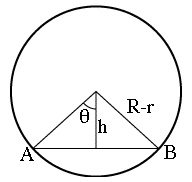
    Nous aurons également besoin de la valeur, modérément précise, de la distance h abaissée du centre O sur la ligne AB , ou plus commodément de l'angle θ (thêta grec ; voir fig. 4 ci-dessous), moitié de l'angle couvert par AB. Son évaluation à partir des photographies éditées (par exemple la version éditée de Fig. 1 de la page précédente, ou des images de parcelles de terrain comme celle fournie par l' U. of Lancashire) donne environ 46.4 degrés. Ainsi (schéma 4 ci-dessous)

Fig. 4   Variables utilisées dans le calcul

Puisque la durée du temps de passage T est proportionnelle à la distance (AB), on peut écrire

où k est un coefficient de proportionnalité. Le calcul de sa valeur ne sera pas nécessaire, puisque notre objectif est d'utiliser le rapport T à la différence ΔT des temps de transits observées de deux endroits différents : dans ce calcul le rapport k est éliminé. Selon la trigonométrie :

    Si la ligne A'B de l'autre station est légèrement plus longue, elle couvre un angle légèrement plus grand de 2(θ+δ), et sa distance de O n'est pas h mais

    Si δ est un angle très petit, sinδ l'est aussi. Mais même si la petite valeur de sinδ reste suffisamment importante pour devoir être prise en compte, cosδ est probablement assez proche de 1 pour pouvoir le remplacer sans risque par 1. Pour le démontrer, il faut se souvenir que :

    Rappelons aussi que "racine carrée" est aussi "puissance 1/2", théorème binomial

    Ainsi si nous assimilons cosδ à 1, l'erreur n'est que de l'ordre de sin²δ ce qui (comme pour les petits nombres) est beaucoup plus petit que sinδ . Si en exprimant h ', nous conservons sinδ mais nous remplaçons cosδ par 1, on obtient avec à une bonne approximation :

    La durée du temps de passage au point P 'est obtenue similairement comme avec l'équation (2)

    et avec la même bonne approximation que précédemment avec le petit angle δ

    Comme on pouvait le prévoir, la petitesse du rapport du côté gauche est équilibrée par celle de sinδ du côté droit. On en extrait :

    Ceci peut être substitué dans l'équation (4) pour D par une autre petite équation :

    C'est ce dont nous avions besoin : Comme Halley l'avait indiqué, la distance D entre le tracé des passages est maintenant exprimé en différence du temps observé entre les passages, aussi bien pour l'intervalle du temps observé T du passage (ou de sa moyenne (T + T') / 2) que pour l'angle θ, donnant la distance du tracé du passage par rapport au centre du soleil.