|
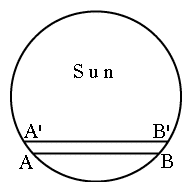
Suppose some observer at point P on Earth sees Venus cross the Sun's disk from A to B (Figure 2 above--two figures, front and side). The motion of Venus across the Sun's disk is due to the combined orbital motions of the two planets; by Kepler's laws, the closer a planet is to the Sun, the faster it moves, so Venus moves faster than Earth, and during a transit essentially overtakes it.
The orbit of Venus is quite close to the orbital plane of Earth, usually known as the plane of the ecliptic (close, but not identical--or else a transit would occur every time Venus overtakes Earth). Therefore the line AB is nearly parallel to the line marking the ecliptic on the celestial sphere, the line along which the plane of the ecliptic intersects our view of the sky.
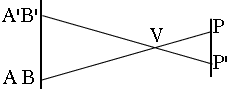
Viewed from a different point P', Venus moves along A'B', essentially parallel to AB. That different point is preferably on the opposite side of the equator, which most likely places it on the opposite side of the ecliptic, too. If we then measure the distance D between AB and A'B', we can in principle apply some simple trigonometry to the parallax and derive the distance PV between P and the position V of Venus.
If only astronomy were so easy! Actually, the lines AB and A'B' are very close to each other. The figure on top of the page (its source is
here) contains images of Venus in front of the Sun, obtained on June 8, 2004, from 3 locations, with each set of data marked in a different color. It is evident the paths are very close, less than a Venus radius apart. Measuring each separately and deriving from that their separation D is not likely to give a very accurate result.
What Halley noted was that equivalent information can be obtained by timing the passage of Venus from A to B and from A' to B'. Because the edge ("limb") of the Sun curves, the length AB differs from that of A'B' (we say "length" for convenience--actually AB, A'B' and D are all visual angles). The apparent velocity of the motion of Venus across the Sun is almost the same when viewed from any location on Earth, so by obtaining the difference in time between the crossing of AB and of A'B', the distance D can also be deduced. This is much more sensitive because the duration of the transit is hours, while the difference in transit time may amount to minutes. Such durations can be (in principle) measured quite accurately.
In these sections we will outline a simplified procedure for deriving the astronomical unit from the transit times on June 8, 2004, using predicted durations of the transits. The astronomers who calculated those durations--available on the web here--used of course the well-established value of the astronomical unit, making this just an exercise. If this had been a "real" calculation, observed values would have been used. This will be a somewhat crude calculation, using simplifying assumptions and neglecting corrections which actual determinations may need.
Since we are free to select observing stations, we choose two at almost the same longitude and at equal latitudes north and south of the equator. They are both in Africa (latitude and longitude within about half a degree)
|
![[IMAGE: Image of Venus Transit]](Sfigs/Venus2.gif)