(12) Kepler's Second Law

            The Law

The ellipse traced by a planet around the Sun has a symmetric shape, but the motion is not symmetric.

    Think of a stone thrown upwards. As it rises it loses speed... then for an instant, at the top of the trajectory, it moves very slowly... and finally it comes down, gathering speed again. In many ways, a planet around the Sun, or of a scientific satellite around Earth, moves like that, too, although the equations are different.

    That is most evident if the orbit is elongated, that is, its eccentricity is large. As the planet or satellite rises in its orbit, it slows down, then as it returns, it speeds up again. It moves fastest during its closest approach, at a point of the orbit called perihelion for a planet ("helios" is the Sun) and perigee for an Earth satellite ("gee" from "geo", denoting Earth-related).

    After studying actual observations, mainly of Mars, Kepler proposed the following prescription for predicting the speeding-up and the slowing-down. Let a line ("radius vector") be drawn from the center of the Sun to the planet (or from the center of Earth to the satellite). Kepler's law states:

"The radius vector sweeps equal areas in equal times"

Illustrating Kepler's 2nd law:  segments AB and CD take  equal times to cover.

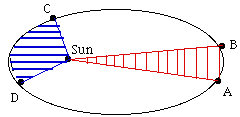
    As an example, let the drawing on the right represent the orbit of an Earth satellite, and let AB and CD be the portions of the orbit covered in 3 hours near apogee and near perigee, respectively. If then O is the Earth's center, the shaded areas OAB and OCD are equal. What it means, obviously, is that CD is much longer than AB, because near perigee the satellite moves much faster and it covers a much greater distance in 3 hours.

            Energy

    Energy may be loosely defined as anything that can make a machine move. The forms of energy which power our machines are usually electricity or heat; light is another form, converted into electricity by the solar cells which power most satellites.

    Gravity can also provide energy. The wheels of grandfather clocks are turned by weights which gradually descend to the bottom of the clock, at which point they have to be cranked up again, or else the clock stops. Thomas Jefferson, at his home near Charlottesville, Virginia, had a clock whose weights (hanging on the side of the room) were cannonballs strung on a rope, and to give the clock a 7-day range, a hole was cut in the floor allowing the balls to descend to the basement.

    When a weight or cannonball is raised against the force of gravity, it has potential energy--energy by virtue of its position, proportional to the height to which it was raised. If the weight is dropped, it loses height and potential energy, but gains speed and kinetic energy, the energy due to speed of motion. Kinetic energy can be converted back to potential, as happens to a roller coaster after it passes the bottom of a dip and climbs up again.

    A similar change occurs when a stone is thrown upwards with some velocity v. If its mass is m (mass will be defined later, for now view it as something related to weight), its kinetic energy can be shown to be

1/2 mv²

As it rises, v and the kinetic energy decrease, but this is matched by the growth of the potential energy

h m g

where h is the height in meters and g is a constant measuring the strength of the force of gravity: if m is in kilograms, h in meters and v in meters-per-second (written m/sec; walking speed is about 1-2m/sec), g is about 9.81.

The sum of the two is the total energy E and stays constant:

E  =   1/2 mv² +  h m g = constant

    As the stone rises, the kinetic part of its energy gets smaller and smaller, becoming zero when it reaches its highest point, where for a brief instant v = 0. On the downward trip, the opposite changes take place. In a later section we will come back to that formula and to the concept of energy.

            The Mean Anomaly

    Earlier it was stated that a third orbital element is needed to specify where in its orbit is the satellite located. Since the equation of the orbital ellipse is

r = a(1 – e²)/(1 + e cos f)

each value of the angle f --called the "true anomaly"--specifies a position along the orbit. One could therefore use the true anomaly as third orbital element.

    The true anomaly f varies periodically around the orbit, quickly near perigee and slowly near apogee. Kepler's second law tells us everything about this variation and should allow us to obtain a formula that gives the way f varies with time t. Unfortunately, no neat way exists for expressing that formula.

    The simplest way of expressing f is to use two auxiliary angles, which like f increase by 360 degrees each orbit, the "eccentric anomaly" E (the letter here has nothing to do with energy) and the "mean anomaly" M; an equation then exists connecting f and E, and another that connects E and M. The great virtue of M is that it grows in proportion to the time t:

M = M(0) + nt

where M(0) is the value of M when t = 0 and n is a constant (related to the constant appearing in Kepler's third law). The mean anomaly is what is counted as the third orbital element.

If one wishes to predict the position of a satellite in its orbit at some time t, assuming the elliptical motion of Kepler's laws is good enough for that prediction (neglecting the pull of the moon, friction of the upper atmosphere etc. ) the first step is to derive M from the above formula. Then E is derived from E, and finally f from E, tasks which electronic computers handle quite easily (though at one time, those calculations were done on paper, not nearly as quickly or easily). The formula for r then gives the position of the satellite in its orbit; all that the computation requires are the elements a, e and M(0), the mean anomaly at t=0.