|
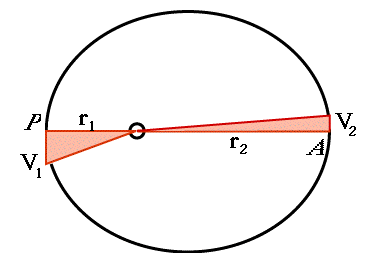
At two points of the orbit the directions of r and V are perpendicular to each other: at the point P of closest approach ("perihelion" for a planet, "perigee" for an Earth satellite), and at the most distant point A ("aphelion" or "apogee"). Let their values be r1 and V1 at P, and r2 and V2 at A.
Imagine an Earth satellite, located at perigee P (see drawing). In one second it will have advanced a distance V1 meters (or whatever units are used). Since that is just a tiny part of the orbit, no great error occurs if, in calculating the area swept by the radius r1, we replace it with a straight line. The swept area is then a long and skinny right-angled triangle with height r1 and base V1 (skinnier than we could draw here, so the drawing is just to give the labeling).
The area A1 of such a triangle, by the formula for areas of right-angled triangles, is one half base time height, or
A1 = (1/2) V1r1
Similarly, the area A2 covered in one second after passing apogee A equals
A2 = (1/2) V2r2
However, by Kepler's 2nd law
A1 = A2
so
(1/2) V1r1 =
(1/2) V2r2
or, multiplying everything by 2
V1r1 =
V2r2
A more useful form of that relation appears if both sides are divided by V2r1 :
V1 / V2 =
r2 / r1
The ratio of velocities equals the inverse of the ratio of distances. The smaller the distance, the faster the motion. If perigee distance is half of the apogee distance, the velocity there is twice as large. (But please remember--this proportionality only holds with P and A, not with other points along the orbit).
Why are Seasons Unequally Spaced?
The main dividing points of the year are the two solstices--longest day in summer, longest night in winter--and the two equinoxes, when night and day are equal. These are the starting points of summer, winter, spring and fall, and it is generally assumed that they are equally spaced.
But are they?
Spring equinox in 2003 was on March 21, while fall equinox was on September 22, 184 days later. In 2004, a leap year, spring equinox occurs March 20, and if you count the days, you will see that to get there only takes 181 days more. The two intervals are not equal.
How can that be? Equinox positions are on opposite sides of the Earth's orbit, 180° apart, yet getting through (northern) winter takes Earth 3 days less than getting through summer.
Because by Kepler's 2nd law, the Earth moves in its orbit a little faster in winter. As noted at the end of "Seasons of the Year" and also in connection with the Milankovich Theory of ice ages, Earth is closest to the Sun--at perihelion--around January 4. By the equations derived here, that's when it moves fastest. Furthermore (see drawing), the half of the ellipse closest to the Sun is also shorter. With Earth the difference is small, since the orbit is quite close to a circle; but it exists, nevertheless, and is the reason for that difference of 3 days.
Note: According to item on Hipparchus in "Wikipedia" (section #4.4) the above asymmetry was known to the ancient Babylonians (Chaldeans), was measured by Hipparchus around 140-130 BC, and was quoted by Ptolemy.
|