Center of Gravity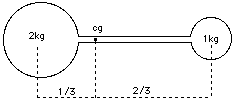
Most people have at least an intuitive notion of the center of gravity (CG) of an object: it is the point on which the object can be perfectly balanced. Grab a broom at one end and the other end tries to drop down; grab it at its center of gravity, and it stays balanced, neither end tipping over. If you have learned to balance a chair or a broom on the palm of your hand, you know the trick is to place your hand right below the center of gravity. Since your hand is not at the CG but below it, it must be constantly moved to keep that strategic position. There also exists a precise mathematical definition--it has nothing to do with gravity, which is why many scientists and engineers prefer the term center of mass. However, it leads off the main subject and therefore we won't bother with it now. A lightweight stick with two balls of equal weight at its end obviously has its CG in the middle. When one ball is twice the weight of the other, the CG divides the distance between them by a ratio 1:2, in a way that makes it closer to the heavier mass (see figure). And similarly for other ratios. Balls that push each other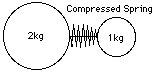
Now imagine that instead of a lightweight stick the above two heavy balls have a spring between them, held compressed by a string. Even though the balls are separate, one can speak of their common center of gravity, on the line connecting their centers, 1/3 of the distance from the center of the heavier ball. (The CG of the Earth-Moon system can be defined in the same manner. Since the ratio of masses of the two bodies is about 81:1, the CG is the point on the line between their centers dividing it by that ratio. It can be shown that--neglecting the pulls of the Sun and of other planets--the Moon does not orbit the center of Earth, but rather the common CG--and so does the Earth, reacting to the pull of the moon. Of course, since the Earth is much more massive, the CG is not very far from the center of the Earth--in fact, it is closer than the Earth's own surface.) Suppose next that a lit match is placed against the string, burning it through. As the spring expands, it pushes the balls apart; if it is sufficiently light, its own motion does not matter and we can assume that the balls push each other. By Mach's formulation of the equations of motion, if the heavy ball receives an acceleration a, then the light one gets 2a, twice as much. For each increment in the velocity of the heavy ball, the light one receives twice as much, and it follows that at any time, its total velocity, as well as the distance covered, are twice those of the heavy ball. Conservation of momentum leads to the same result. If then the heavy ball is at a distance D from the initial position of the spring, the light one is at distance 2D--as in the earlier figure, reproduced here. No matter how much time passes, the center of gravity stays at the same spot. RocketsThat turns out to be a very general principle: in any object or collection of objects, forces which only involve those objects and nothing else ("internal forces") cannot shift the center of gravity. An astronaut floating in a space suit cannot shift his position without involving something else, e. g. pushing against his spacecraft. The center of gravity--or "center of mass"--is a fixed point, which cannot be moved without outside help (turning around it, however, is possible). By throwing a heavy tool in one direction, the astronaut could get moving in the opposite direction, though the common center of gravity of the two would always stay the same. Given a bottle of compressed oxygen, the same result follows from squirting out a blast of gas (a scene that appeared in an early science fiction film). A rocket does much the same, except that the cold gas is replaced by the much faster jet of glowing gas produced by the burning of suitable fuel.
The powerful rockets which lift hundreds or even thousands of tons off the launching pad depend on the same principle. If you ever watched a rocket lift off at Cape Canaveral, it is worth remembering that if you could somehow remove from the scene the launching pad, the atmosphere and the Earth, then the combined center of gravity of the rocket and its exhaust gases would always remain where it started, at the launching point. It may seem like a round-about way for producing motion. And yet, rockets are (at least for now) the only practical means of leaving Earth and flying into space. --------------------------
Rocket MotionSuppose we have a rocket of total mass 2M, of which M is payload and M is fuel. As the fuel is burned, it is ejected with an average velocity V relative to what the rocket had at the start.
To avoid this (the full derivation requires calculus) let us just define the mean velocity V by conservation of momentum, without trying to puzzle out its relation to the jet speed v. At burn-out, we say, the jet has imparted momentum MV to the payload, and has itself carried an equal and opposite momentum backwards.] The payload now has gained velocity V. But we need more! So we build a rocket of mass 4M, of which 2M is fuel, while the payload, also of mass 2M, is the smaller rocket described above, serving as second stage. When the fuel of the big rocket is finished, we reach a velocity V, then the second stage is ignited, adding another V to the velocity, for a total of 2V. Still faster! Now the rocket has mass 8M of which 4M is fuel of the first stage, while 4M is the two-stage rocket of the preceding design. The first stage gives velocity V, to which the other two add 2V, for a total of 3V. By now you can see the trend. If the mass of the final payload is M, then
Each time the velocity increases by one notch, the mass doubles. One cannot avoid this sort of thing by giving up staging--say, in the rocket of mass 8M, by firing all the 7M of fuel in one blast. That is because (as already noted), as the payload (+ remaining fuel) gain speed, less and less momentum is transferred, the jet first having to overcome the forward motion, Indeed, the correct derivation (which uses calculus) gives the equivalent of a huge number of little stages, fired one after the other. The same exponential result is still obtained. This is one of the great problems of spaceflight, especially with the first stages which rise from the ground: even a small payload requires a huge rocket. Perhaps some day space explorers will be able to shave off some fuel weight by using air-breathing rockets ("scramjets") but those seem practical only for the lowest 1/4 to 1/3 of the orbital velocity. Launching from a high-flying airplane--like Burt Rutan's "SpaceshipOne", or the "Pegasus" solid-fuel rocket, used in launching some small satellites--also helps cut air resistance, another factor. But no other shortcuts are in sight. Once in orbit, of course, more efficient but more gradual ways of generating thrust can be enlisted, like ion propulsion.
-----------------------------------------------------
|
