Максимальная
несмешанность. Максимальная
несмешанность - это критерий планирования
эксперимента, который является частью критерия
плана разрешения. Критерий максимальной
несмешанности определяет такие генераторы
плана, что при заданном разрешении
максимальное число взаимодействий
с порядком, не большим критического, является
несмешиваемым со всеми остальными
взаимодействиями. Этот критерий является
альтернативой критерию минимальной
аберрации при поиске "наилучшего" плана
максимального разрешения. За обсуждением роли
критерия в планировании эксперимента обратитесь
к разделам 2**(k-p) дробные
факторные планы и Поиск
лучшего 2**(k-p) дробного факторного плана.
Маргинальные частоты. В многовходовой таблице значения, расположенные на краях таблицы - это просто одномерные таблицы частот рассматриваемых переменных. Для таблицы с двумя входами они записываются в самом правом столбце и самой нижней строке. Маргинальные значения важны, так как позволяют оценить распределение частот в отдельных столбцах и строках таблицы. Различия в распределении частот в строках (или столбцах) отдельных переменных и в соответствующих маргинальных частотах дают информацию о зависимости табулированных переменных.
За дополнительной информацией о маргинальных
частотах обратитесь к разделу Кросстабуляции
в главе Основные
статистики.
Масса (в анализе
соответствий). Термин "масса" в анализе соответствий
используется для обозначения относительных
частот, содержащихся ячейках двухвходовой
таблицы (число исходных наблюдений в каждой
ячейке делится на сумму всех наблюдений в
таблице). Заметим, что результаты анализа соответствий также
верны, если ячейки таблицы содержат не
относительные частоты, а другие меры
соответствия, связи, подобия и т.д. Поскольку
сумма всех ячеек таблицы относительных частот
равна 1.0, то можно сказать, что данная таблица
показывает, как распределена единичная масса по
ячейкам таблицы (аналог плотности
распределения). В терминологии анализа
соответствий, суммы по строкам и столбцам в
матрице относительных частот называются массой
строки и массой столбца, соответственно.
Масштабируемое
программное обеспечение. Относящиеся к
этой категории программные продукты (например,
системы управления базами данных MS SQL или Oracle)
можно расширить в соответствии с новыми
требованиями без нарушения структуры их
операций (например, расщепления данных на более
мелкие фрагменты), что позволяет избежать
снижения их эффективности. Например,
администратор расширяемой сети может добавлять
новые узлы, не изменяя основную систему. Примером
нерасширямой системы является структура
директорий DOS (добавляемые файлы обязательно
распределяются по поддиректориям). См. также
раздел Программное
обеспечение на производстве.
Матрица Берта. Многомерный анализ соответствий использует как входной формат данных (т.е. преобразует произвольные данные к такому формату) так называемую матрицу Берта. Матрица Берта является квадратом бинарной матрицы. Если вы обозначите данные (бинарную матрицу) в рассматриваемом примере как матрица X, то матричное произведение X'X является матрицей Берта. Ниже приведена матрица Берта для данного примера.
| ВРЕМЯ ЖИЗНИ | ВОЗРАСТ | ГОРОД | ||||||
|---|---|---|---|---|---|---|---|---|
| NO | YES | <50 | 50-69 | 69+ | ТОКИО | БОСТОН | ГЛАМОРН | |
| ВЫЖИЛ:НЕТ ВЫЖИЛ:ДА ВОЗРАСТ:ДО_50 ВОЗРАСТ:ОТ_50ДО69 ВОЗРАСТ:СВЫШЕ_69 ГОРОД:ТОКИО ГОРОД:БОСТОН ГОРОД:ГЛАМОРН |
210 0 68 93 49 60 82 68 |
0 554 212 258 84 230 171 153 |
68 212 280 0 0 151 58 71 |
93 258 0 351 0 120 122 109 |
49 84 0 0 133 19 73 41 |
60 230 151 120 19 290 0 0 |
82 171 58 122 73 0 253 0 |
68 153 71 109 41 0 0 221 |
Данная матрица симметрична. В случае 3-х
группирующих переменных (как и в рассматриваемом
примере) матрица данных состоит из 3 x 3 = 9 блоков,
которые образуются в результате взаимной
кросстабуляции имеющихся группирующих
переменных. Заметим, что суммы диагональных
элементов каждого диагонального блока (т.е. в тех
блоках, где переменные кросстабулированы сами с
собой) постоянны и равны 764 для каждого случая.
Все внедиагональные элементы, принадлежащие
диагональным блокам, равны 0. Если же объекты
некоторой матрицы плана кодировались с помощью
процедуры нечеткого кодирования (т.е. если
принадлежность объекта категории определялась
некоторой вероятностью), то равенство 0
внедиагональных элементов диагональных блоков
не гарантировано.
Матрица
несоответствий (для нейронных сетей). В
задачах классификации так
иногда называют матрицу, в которой для каждого
класса наблюдений приводится количество
наблюдений, отнесенных сетью
к этому и другим классам. В пакете Нейронные
сети STATISTICA выводится как одна из статистик
классификации.
Матрица потерь. Квадратная матрица, при умножении которой на вектор вероятностей принадлежности классам получается вектор оценок потерь от ошибок классификации; на основе этого вектора можно принимать решения, приводящие к наименьшим потерям.
См. также раздел о нейронных
сетях.
Матричные графики.
На матричных графиках изображаются зависимости
между несколькими переменными в форме матрицы
XY-графиков. Наиболее распространенным типом
матричного графика является матрица диаграмм рассеяния, которую
можно считать графическим эквивалентом корреляционной матрицы.
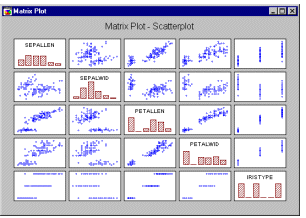
Матричные графики - Диаграммы рассеяния. На матричном графике этого типа изображаются 2М диаграммы рассеяния, организованные в форме матрицы (значения переменной по столбцу используются в качестве координат X, а значения переменной по строке - в качестве координат Y). Гистограммы, изображающие распределение каждой переменной, располагаются на диагонали матрицы (в случае квадратных матриц) или по краям (в случае прямоугольных матриц).

См. также раздел Сокращение объема выборки.
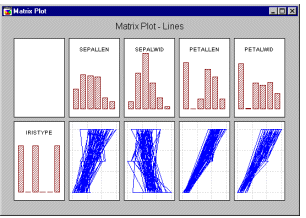
Матричные
графики - Линейные графики. Этот тип
матричных графиков представляет собой матрицу X-Y
линейных (т.е. не последовательных) графиков
(похожую на матрицу диаграмм рассеяния), где
отдельные точки данных соединены линиями в
порядке их появления в файле данных. Гистограммы,
изображающие распределение каждой переменной,
расположены по диагонали матрицы (в квадратных
матрицах) или по краям (в прямоугольных матрицах,
см. следующий рисунок).
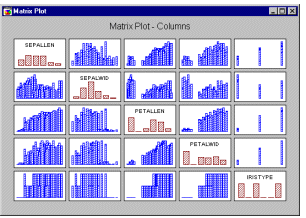
Матричные графики - Столбчатые диаграммы. На матричном графике этого типа столбцы представляют собой проекции отдельных точек данных на ось X (они показывают распределение максимальных значений). Гистограммы, изображающие распределение каждой переменной, расположены по диагонали матрицы (в квадратных матрицах) или по краям (в прямоугольных матрицах).
Медиана. Медиана выборки (термин был впервые введен Гальтоном, 1882) - это значение, которое разбивает выборку на две равные части. Половина наблюдений лежит ниже медианы, и половина наблюдений лежит выше медианы. Медиана вычисляется следующим образом. Изучаемая выборка упорядочивается в порядке возрастания. Получаемая последовательность ak, где k=1,..., 2*m+1называется вариационным рядом или порядковыми статистиками. Если число наблюдений нечетно, то медиана оценивается как: am+1. Если число наблюдений четно, то медиана оценивается как:
m= |
am+am+1 |
2 |
См. также раздел Описательные
статистики.
Мера DFFITS.
Несколько методов доступны для проверки воздействия и влияния
определенного наблюдения в регрессии (включая стьюдентизированные
остатки, стьюдентизированные
удаленные остатки, DFFITS, стандартизованные
DFFITS). Белсли (Belsley et al., 1980) предложил
использовать DFFITS как меру, которая приписывает
больший вес выбросам, чем расстояние
Кука. DFFITS вычисляется по формуле
DFFITi = ![]() iei/(1-
iei/(1-![]() i)
i)
где
ei ошибка для i-го
наблюдения
hi i-е воздействие
(диагональный элемент матрицы (X(X'X)X')))
![]() i =
1/N + hi.
i =
1/N + hi.
Более подробная информация дана в работах Hocking
(1996) и Ryan (1997).
Метод
взвешенных наименьших квадратов (в регрессии).
В некоторых случаях при проведении
регрессионного анализа желательно приписать
различным наблюдаемым значениям разные веса и
вычислить так называемые оценки метода
взвешенных наименьших квадратов. Этот метод
часто применяется в ситуациях, когда дисперсия
остатков не постоянна на области значений
независимой переменной. Тогда мы можем приписать
остаткам веса, равные обратным величинам
соответствующей дисперсии, и получить оценки
взвешенных наименьших квадратов. (На практике
эти дисперсии обычно не известны, однако часто
они пропорциональны значениям независимых
переменных, и эта пропорциональность может быть
использована для вычисления подходящих весов
наблюдений.) В работе Neter, Wasserman and Kutner (1985) описан
пример такого анализа.
Метод
максимума правдоподобия. Метод максимума
правдоподобия (термин был впервые использован в
работе Фишера, 1922) - это общий метод оценивания
параметров генеральной совокупности с помощью
максимизации функции правдоподобия (L)
выборки. Функция правдоподобия L выборки из n
наблюдений x1, x2, ..., xn в
случае дискретного распределения переменных x1,
x2, ..., xn описывается функцией
совместного распределения p(x1, x2,
..., xn). Если x1, x2, ..., xn
имеют непрерывное распределение, функция
правдоподобия L выборки из n наблюдений x1,
x2, ..., xn описывается совместной
плотностью распределения f(x1, x2,
..., xn).
Пусть L - функция правдоподобия выборки; при
наблюдаемых значениях x1, x2, ..., xn
L является функцией параметров ![]() 1,
1, ![]() 2, ...
2, ... ![]() k.
Тогда оценками максимального правдоподобия
k.
Тогда оценками максимального правдоподобия ![]() 1,
1, ![]() 2, ...
2, ... ![]() k
называются значения параметров
k
называются значения параметров ![]() 1,
1, ![]() 2, ...
2, ... ![]() k,
максимизирующие функцию L. Очевидно, оценки
зависят от наблюдений x1, x2, ..., xn.
В широких предположениях эти оценки являются
оптимальными.
k,
максимизирующие функцию L. Очевидно, оценки
зависят от наблюдений x1, x2, ..., xn.
В широких предположениях эти оценки являются
оптимальными.
Пусть ![]() -
это элемент пространства
-
это элемент пространства ![]() . Если
. Если ![]() - открытый интервал, а L(
- открытый интервал, а L(![]() )
дифференцируема и достигает максимума на
)
дифференцируема и достигает максимума на ![]() , то оценки
МП удовлетворяют уравнению (dL(
, то оценки
МП удовлетворяют уравнению (dL(![]() ))/d
))/d![]() = 0. Для
получения дополнительной информации см.
например, книги А.А.Боровков "Математическая
статистики: оценка параметров, проверка гипотез"
(1984), Г.И.Ивченко, Ю.И.Медведев "Статистика"
(1992) или работы Mendenhall and Sincich (1984), Bain and Engelhardt (1989) и
Neter, Wasserman, and Kutner (1989).
= 0. Для
получения дополнительной информации см.
например, книги А.А.Боровков "Математическая
статистики: оценка параметров, проверка гипотез"
(1984), Г.И.Ивченко, Ю.И.Медведев "Статистика"
(1992) или работы Mendenhall and Sincich (1984), Bain and Engelhardt (1989) и
Neter, Wasserman, and Kutner (1989).
См. также разделы Нелинейное
оценивание и Компоненты
дисперсии и смешанная модель ANOVA/ANCOVA.
Метод
моментов. С помощью этого метода можно
оценить неизвестные параметры распределения (см.
разделы Графики
квантиль-квантиль, Графики
вероятность-вероятность и Анализ процессов). Метод
моментов приравнивает моменты теоретического
распределения к моментам эмпирического
распределения (распределения, построенного по
наблюдениям). Из полученных уравнений находятся
оценки параметров распределения. Например, для
распределения с двумя параметрами первые два
момента (среднее и дисперсия распределения,
соответственно, ![]() и
и ![]() )
будут приравнены первым двум эмпирическим
(выборочным) моментам (среднему и дисперсии
выборки, соответственно, несмещенным оценкам x-bar
и s**2), и затем будет произведено оценивание. С
другой стороны, для оценки параметров вы можете
воспользоваться методом
максимального правдоподобия. Метод
максимального правдоподобия позволяет строить
более точные (эффективные) оценки, чем метод
моментов. За дополнительной информацией
обратитесь к работе Hahn and Shapiro, 1994.
)
будут приравнены первым двум эмпирическим
(выборочным) моментам (среднему и дисперсии
выборки, соответственно, несмещенным оценкам x-bar
и s**2), и затем будет произведено оценивание. С
другой стороны, для оценки параметров вы можете
воспользоваться методом
максимального правдоподобия. Метод
максимального правдоподобия позволяет строить
более точные (эффективные) оценки, чем метод
моментов. За дополнительной информацией
обратитесь к работе Hahn and Shapiro, 1994.
Метод
наименьших квадратов. Общий смысл
оценивания по методу наименьших квадратов
заключается в минимизации суммы квадратов
отклонений наблюдаемых значений зависимой
переменной от значений, предсказанных моделью.
Более точно, оценки наименьших квадратов (НК)
параметра q получаются минимизацией функции Q по ![]() ,
где:
,
где:
Q = ![]() [Yi - fi(
[Yi - fi(![]() )]2
)]2
Отметим, что fi(![]() ) -
это известная функция
) -
это известная функция ![]() , Yi = fi(
, Yi = fi(![]() ) +
) + ![]() i,
где i = от 1 до n,
i,
где i = от 1 до n, ![]() i
- это случайные величины (например, погрешности
измерений), средние которых обычно полагаются
равными 0.
i
- это случайные величины (например, погрешности
измерений), средние которых обычно полагаются
равными 0.
Для получения дополнительной информации см.
книги А.А.Боровков "Математическая статистики:
оценка параметров, проверка гипотез" (1984), Г.И.Ивченко,
Ю.И.Медведев "Статистика" (1992) или работы
Mendenhall and Sincich (1984), Bain and Engelhardt (1989) и Neter, Wasserman, and Kutner
(1989). См. также разделы Основные
статистики, Множественная
регрессия и Нелинейное
оценивание.
Метод
Розенброка. Этот метод нелинейного оценивания
вращает пространство параметров, располагая
одну ось вдоль "гребня" поверхности (он
называется также методом вращения координат -
method of rotating coordinates), при этом все другие остаются
ортогональными выбранной оси. Если поверхность
графика функции потерь
имеет одну вершину и различимые "гребни" в
направлении минимума этой функции , то данный
метод приводит к очень точным значениям
параметров, минимизирующим функцию потерь.
Метод
сопряженных градиентов. Быстродействующий
алгоритм обучения многослойных
персептронов, осуществляющий
последовательный линейный поиск в пространстве
ошибок. Последовательные направления поиска
выбираются сопряженными (не противоречащими
друг другу), см. Bishop, 1995.
Метод
Хука-Дживиса. Метод нелинейного
оценивания, который при каждой итерации
сначала определяет схему расположения
параметров, оптимизируя текущую функцию потерь
перемещением каждого параметра по отдельности.
При этом вся комбинация параметров сдвигается на
новое место. Это новое положение в m-мерном
пространстве параметров определяется
экстраполяцией вдоль линии, соединяющей текущую
базовую точку с новой. Размер шага этого процесса
постоянно меняется для попадания в оптимальную
точку. Этот метод обычно очень эффективен, и его
следует использовать в том случае, когда ни квази-ньютоновский,
ни симплекс-метод не
дают удовлетворительных оценок.
Минимакс. Алгоритм определения коэффициентов линейного масштабирования для набора чисел. Находятся минимальное и максимальное значения, затем масштабирующие коэффициенты выбираются таким образом, чтобы преобразованный набор данных имел заранее заданные минимальное и максимальное значения.
См. также раздел Нейронные
сети.
Минимальная
аберрация. Минимальная аберрация
- это критерий планирования эксперимента,
который является частью критерия разрешения.
План минимальной аберрации определяется, как
план максимального разрешения,
"который минимизирует число слов минимальной
длины в определяемом отношении" (Fries & Hunter,
1984). Другими словами, критерий минимальной
аберрации определяет такие генераторы плана,
которые дают наименьшее число пар смешанных взаимодействий критического
порядка. За обсуждением роли критерия в
планировании эксперимента обратитесь к разделам
2**(k-p) дробные факторные планы
и Поиск лучшего 2**(k-p)
дробного факторного плана.
Многомерное шкалирование. Многомерное шкалирование (МНШ) можно рассматривать как альтернативу факторному анализу (см. Факторный анализ), и обычно оно используется для разведочного анализа данных. Целью последнего, вообще говоря, является поиск и интерпретация "латентных (т.е. непосредственно не наблюдаемых) переменных", дающих возможность пользователю объяснить сходства между объектами, заданными точками в исходном пространстве признаков. В факторном анализе сходства между объектами (например, переменными) выражаются с помощью матрицы (таблицы) коэффициентов корреляций. В методе МНШ дополнительно к корреляционным матрицам, в качестве исходных данных можно использовать произвольный тип матрицы сходства или различия объектов (включая несовместные множества мер, например, не следующие аксиоме транзитивности).
Подробнее см. раздел главу Многомерное
шкалирование.
Многомерные дихотомии. Одним из способов кодирования ответов, когда возможно более одного ответа на поставленный вопрос, является кодирование с использованием многомерных дихотомий. Представьте, что в процессе большого маркетингового исследования, вы попросили покупателей назвать 3 лучших, с их точки зрения, безалкогольных напитка. Обычный вопрос может выглядеть следующим образом:
Напишите ниже три ваших любимых
безалкогольных напитка:
1:__________ 2:__________ 3:__________
Предположим далее, что вас интересуют только Coke,
Pepsi и Sprite. Одним очевидным способом кодирования
является следующий:
| COKE | PEPSI | SPRITE | . . . . | |
|---|---|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 . . . |
1 . . . |
1 1 . . . |
1 . . . |
Здесь каждая переменная используется для одного
напитка. Код 1 будет введен в таблицу в
переменную всякий раз, когда соответствующий
респондент указал ее в своем ответе. Заметим, что
каждая переменная является дихотомией, т.е.
принимает только два значения: "1" и "не
1" (можно ввести 1 и 0, но так обычно
не делается, можно просто рассматривать 0 как
пустую ячейку или пропуск). Когда табулируются
такие значения, вы получите итоговую таблицу, из
которой можете вычислить число и процент
респондентов (и ответов) для каждого напитка.
Таким образом, вы компактно представили три
переменные Coke, Pepsi, Sprite одной переменной - многомерной
дихотомией.
За дополнительной информацией о многомерных
дихотомиях обратитесь к разделу Таблицы
многомерных откликов в главе Основные статистики.
Многомерные отклики. Кодирование ответов переменными с многомерными откликами необходимо, когда возможен более, чем один ответ на поставленный вопрос. Представьте, что в процессе большого маркетингового исследования, вы попросили покупателей назвать 3 лучших, с их точки зрения, безалкогольных напитка. Обычный вопрос может выглядеть следующим образом:
Напишите ниже три ваших любимых
безалкогольных напитка:
1:__________ 2:__________ 3:__________
Анкета содержит от 0 до 3 ответов. Очевидно, список
напитков может быть очень большим. Ваша цель -
свести результаты в таблицу, в которой, например,
будет подсчитан процент респондентов,
предпочитающих определенный напиток. Более
разумным является следующий подход. Введите 3
переменные с многомерными откликами и
определите схему кодирования для 50 напитков.
Затем введите соответствующие коды
(альфа метки) для значений переменных и получите
таблицу вида:
| Ответ 1 | Ответ 2 | Ответ 3 | |
|---|---|---|---|
| наблюдение 1 наблюдение 2 наблюдение 3 . . . |
COKE SPRITE PERRIER . . . |
PEPSI SNAPPLE GATORADE . . . |
JOLT DR. PEPPER MOUNTAIN DEW . . . |
За дополнительной информацией о многомерных
дихотомиях обратитесь к разделу Таблицы
многомерных откликов в главе Основные статистики.
Многослойные
персептроны. Нейронные
сети с прямой передачей сигнала, линейными PSP-функциями и (как правило)
нелинейными функциями активации.
Многоцветная
столбчатая диаграмма. Многоцветные
столбчатые диаграммы могут быть использованы
для представления значений переменной для
данных того же типа, что и в круговой диаграмме.
Однако в данном случае последовательные
значения переменной X отображаются высотами
последовательных вертикальных столбцов, каждый
из которых имеет свой собственный цвет и шаблон
(а не круговыми секторами различной ширины).
Множественная регрессия. Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона, 1908) состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной (откликом).
Общая вычислительная задача, которую требуется решать при анализе методом множественной регрессии, состоит в подгонке прямой линии (или плоскости в n-мерном пространстве, где n - это число независимых переменных) к некоторому набору точек. В простейшем случае, когда имеется одна зависимая и одна независимая переменная, это можно увидеть на диаграмме рассеяния (диаграммы рассеяния - это двумерные графики значений пар переменных). Множественная регрессия используется для проверки гипотез и разведочного анализа.
Для получения дополнительной информации см.
раздел Множественная
регрессия.
Множественный
коэффициент корреляции R. Множественный
коэффициент корреляции R (множественное R) - это
положительный квадратный корень из R-квадрата
(множественного коэффициента детерминации, см. Остаточная дисперсия и
коэффициент детерминации R-квадрат). Эта
статистика полезна при проведении многомерной
регрессии (т.е. использовании нескольких
независимых переменных), когда необходимо
описать зависимость между одной и несколькими
переменными. Принимает значения от 0 до 1.
Является обобщением обычного коэффициента
корреляции.
Множители, увеличивающие дисперсию (VIF). Отметим, что диагональные элементы матрицы, обратной к матрице корреляций (т.е. -1 умноженной на диагональные элементы матрицы выметания) для переменных, входящих в уравнение иногда также называют множителями, увеличивающими дисперсию - variance inflation factors (VIF; см., например, работу Neter, Wasserman, Kutner, 1985). Эта терминология обязана своим появлением тому факту, что дисперсии стандартизованных коэффициентов регрессии можно вычислить как произведение дисперсии остатков (для модели с преобразованными корреляциями) на соответствующие диагональные элементы матрицы, обратной к матрице корреляции. Если предикторы не коррелированы, диагональные элементы обратной к корреляционной матрицы равны 1.0; поэтому для коррелированных предикторов эти элементы представляют "увеличивающие множители" дисперсий коэффициентов регрессии, создаваемые избыточностью предикторов.
См. также раздел Множественная
регрессия.
Мода. Мода выборки (термин был впервые введен Пирсоном, 1894) - это значение, наиболее часто встречающееся в выборке.
См. также раздел Описательные
статистики.
Мультимодальное распределение. Распределение, имеющее несколько мод (т.е. два или более "пика").
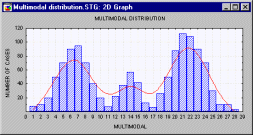
Мультимодальность распределения выборки часто
является показателем того, что распределение не
является нормальным. Мультимодальность
распределения дает важную информацию о природе
исследуемой переменной. Например, если
переменная представляет собой предпочтение или
отношение к чему-то, то мультимодальность может
означать, что существуют несколько определенных
высказываемых мнений. Тем не менее,
мультимодальность часто может показывать, что
выборка не является однородной и наблюдения
порождены двумя или более "наложенными"
распределениями. Иногда мультимодальность
распределения означает, что выбранные
инструменты не подходят для измерения (например
"проблемы разметки" в естественных
науках,"смещенные ответы" в социальных).
См. также разделы унимодальное
и бимодальное
распределение.
Мультипликативная
сезонность, демпфированный тренд. В этой
модели анализа временных
рядов прогнозы простого экспоненциального
сглаживания "улучшаются" демпфированным
трендом [сглаживается независимо с параметром ![]() ] и
аддитивной сезонной компонентой (сглаживается с
параметром
] и
аддитивной сезонной компонентой (сглаживается с
параметром ![]() ). Например, пусть вы прогнозируете процент
семей, имеющих определенное электронное
устройство (например, видеомагнитофон). Каждый
год доля семей, имеющих собственный
видеомагнитофон, увеличивается, однако этот
тренд демпфированный (иными словами, возрастание
тренда постепенно уменьшается) так как с
течением времени рынок насыщается.
Дополнительно, имеется сезонная составляющая
покупательского спроса (спрос меньше в летние
месяцы и больше в Декабре). Эта сезонная
компонента может быть мультипликативной;
например, покупки видеомагнитофона в декабре
возросли в 1.4 раза (на 40%) по сравнению с средними
годовыми продажами.
). Например, пусть вы прогнозируете процент
семей, имеющих определенное электронное
устройство (например, видеомагнитофон). Каждый
год доля семей, имеющих собственный
видеомагнитофон, увеличивается, однако этот
тренд демпфированный (иными словами, возрастание
тренда постепенно уменьшается) так как с
течением времени рынок насыщается.
Дополнительно, имеется сезонная составляющая
покупательского спроса (спрос меньше в летние
месяцы и больше в Декабре). Эта сезонная
компонента может быть мультипликативной;
например, покупки видеомагнитофона в декабре
возросли в 1.4 раза (на 40%) по сравнению с средними
годовыми продажами.
Для вычисления сглаженных значений в первом
сезоне необходимы начальные значения сезонных
компонент. По умолчанию модуль Временные ряды
оценит эти значения (для всех моделей с сезонной
компонентой) из данных с помощью Классической
сезонной декомпозиции. Далее S0 и T0
(начальный тренд) вычисляются по формуле:
T0 = (1/![]() )*Mk-M1)/[(k-1)*p]
)*Mk-M1)/[(k-1)*p]
где
![]() параметр сглаживания
параметр сглаживания
k число полных сезонных
циклов
Mk среднее на
последнем сезонном цикле
M1 среднее на первом
сезонном цикле
p длина сезонного цикла
и S0 = M1-p*T0/2
Мультипликативная
сезонность, линейный тренд. В этой модели
анализа временных рядов
простое экспоненциальное сглаживание
применяется для прогноза обеих компонент:
линейного тренда [сглаживается с параметром ![]() ] и
мультипликативной сезонной компоненты
[сглаживается с параметром
] и
мультипликативной сезонной компоненты
[сглаживается с параметром ![]() ]. Например, пусть
планируется месячный бюджет удаления снежных
заносов в определенном районе. Очевидно, имеется
трендовая компонента бюджета (определяемая
размером района, т.к. имеется устойчивый
возрастающий тренд возрастания затрат в
зависимости от размера района). В то же время,
очевидно, в ряде имеется сезонная составляющая,
отражающая различную вероятность выпадения
снега в разные месяцы года. Эта компонента может
быть мультипликативной, когда расходы в зимние
месяцы должны быть увеличены, например, в 1.4 раза.
]. Например, пусть
планируется месячный бюджет удаления снежных
заносов в определенном районе. Очевидно, имеется
трендовая компонента бюджета (определяемая
размером района, т.к. имеется устойчивый
возрастающий тренд возрастания затрат в
зависимости от размера района). В то же время,
очевидно, в ряде имеется сезонная составляющая,
отражающая различную вероятность выпадения
снега в разные месяцы года. Эта компонента может
быть мультипликативной, когда расходы в зимние
месяцы должны быть увеличены, например, в 1.4 раза.
Для вычисления сглаженных значений в первом
сезоне необходимы начальные значения сезонных
компонент. По умолчанию модуль Временные ряды
оценит эти значения (для всех моделей с сезонной
компонентой) из данных с помощью Классической
сезонной декомпозиции. Далее S0 и T0
(начальный тренд) вычисляются по формуле:
T0 = (Mk-M1)/((k-1)*p)
где
k число полных сезонных
циклов
Mk среднее на последнем
сезонном цикле
M1 среднее на первом
сезонном цикле
p длина сезонного цикла
и S0 = M1 - T0/2
Мультипликативная
сезонность, с исключенным трендом. Эта
модель в анализе временных
рядов частично эквивалентна модели простого
экспоненциального сглаживания. Однако,
дополнительно в каждом прогнозе учитывается
мультипликативная сезонная компонента, которая
сглаживается независимо (см. Параметр сезонного
сглаживания ![]() ). Эта модель могла бы, например,
подойти для прогноза месячных ожидаемых продаж
определенной игрушки. Уровень продаж может быть
достаточно стабильным из года в год или очень
медленно меняться, в то же время имеются
изменения в зависимости от сезона (например,
больше продаж приходится на декабрь). Сезонные
изменения могут влиять на продажи
мультипликативно, например, в зависимости от
общего уровня продаж. Декабрьские продажи всегда
больше в 1.4 раза.
). Эта модель могла бы, например,
подойти для прогноза месячных ожидаемых продаж
определенной игрушки. Уровень продаж может быть
достаточно стабильным из года в год или очень
медленно меняться, в то же время имеются
изменения в зависимости от сезона (например,
больше продаж приходится на декабрь). Сезонные
изменения могут влиять на продажи
мультипликативно, например, в зависимости от
общего уровня продаж. Декабрьские продажи всегда
больше в 1.4 раза.
Мультипликативная
сезонность, экспоненциальный тренд. В этой
модели анализа временных
рядов простое экспоненциальное сглаживание
применяется для обеих компонент:
экспоненциального тренда [сглаживается с
параметром ![]() ] и мультипликативной сезонной компоненты
[сглаживается с параметром
] и мультипликативной сезонной компоненты
[сглаживается с параметром ![]() ]. Например, пусть вы
прогнозируете месячный доход курортной зоны.
Каждый год доход может увеличиваться на
определенный процент или в определенное число
раз (что приводит к экспоненциальному тренду).
Кроме того, в данных, возможно, присутствует
мультипликативная сезонная компонента,
например, доход увеличивается на 20% в декабре по
сравнению с другими месяцами.
]. Например, пусть вы
прогнозируете месячный доход курортной зоны.
Каждый год доход может увеличиваться на
определенный процент или в определенное число
раз (что приводит к экспоненциальному тренду).
Кроме того, в данных, возможно, присутствует
мультипликативная сезонная компонента,
например, доход увеличивается на 20% в декабре по
сравнению с другими месяцами.
Для вычисления сглаженных значений в первом сезоне необходимы начальные значения сезонных компонент. По умолчанию модуль Временные ряды оценит эти значения (для всех моделей с сезонной компонентой) из данных с помощью Классической сезонной декомпозиции. Далее S0 и T0 (начальный тренд) вычисляются по формуле:
T0 = exp{[log(Mk)-log(M1)]/p}
где
k число полных сезонных
циклов
Mk среднее на
последнем сезонном цикле
M1 среднее на первом
сезонном цикле
p длина сезонного цикла
и S0 = exp{log(M1)-p*log(T0)/2}