A different derivation--shorter, more elegant, more general but using vectors and working in a rotating frame of reference--can be found in section (34c). The other two Lagrangian points, L4 and L5, are on the Earth's orbit, with the lines linking them to the Sun making 60° angles with the Earth-Sun line. At those locations the two-body calculation based on the Earth and the Sun also predicts station-keeping (that is, equilibrium in a frame of reference rotating with the Earth). Again, however, L4 and L5 are so distant that for a realistic calculation of the motion of a spacecraft near them, the pull of other planets must be included. However, the Earth-Moon system also has its L4 and L5 points, and these have received some attention as possible sites for observatories and for self contained "space colonies." They have an important property (which will not be proved) that they are stable. In contrast, equilibrium at the L1 and L2 points is unstable, like that of a marble perched atop a bowling ball. If positioned exactly on the top, the marble will stay in place, but the slightest push will make it move further and still further from equilibrium, until it falls off. By contrast, the equilibrium at L4 or L5 are like that of a marble at the bottom of a spherical bowl: given a slight push, it rolls back again. Thus the spacecraft at L4 or L5 do not tend to wander off, unlike those at L1 and L2 which require small onboard rockets to nudge them back into place from time to time. Here we will show that L4 and L5 of the Earth-Moon system are positions of equilibrium in a frame of reference rotating with the Moon, assuming that the Moon's orbit is circular. Non-circular orbits and the question of stability are beyond the scope of this discussion.
Tools of the Calculation
and it is easy to check that the sum of these distances is c and their ratio is m/M. An alternative form of DB (which will be useful) is obtained by dividing numerator and denominator by M:
From trigonometry we will need the "law of sines". Suppose we are given a triangle ABC of arbitrary size and shape (drawing). The angles at the three corners will be named A, B and C as well, while the lengths of the sides facing them are denoted a, b and c. Then the law of sines says
sinA = h/ b b sinA = h and dividing both sides by ab gives the required result. To prove that the angle C also fulfils the condition, we repeat the calculation with a perpendicular line drawn from A or from B. We also need a trigonometrical identity for the sine of the sum of two angles. If those angles are denoted by the Greek letters α and β
The proof of this identity is given separately. Finally, we will need the resolution of vectors (see sec. 14). Suppose a force F acts on an object at some point C, making an angle αwith the direction of a given line, marked here with R (drawing). Suppose also that we need to resolve F into components parallel and perpendicular to R. In the triangle CPQ, if CP represents the force F, then CQ and QP represent its parallel and perpendicular components. Then since
Conditions of Equilibrium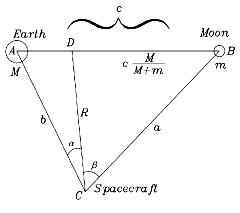 To the diagram drawn earlier to illustrate the center of mass of the Earth-Moon system, we add a spacecraft at some point C, with distances b from the Earth, a from the Moon and R from the center of mass D. As in the derivation of the law of sines, we name (A,B,C) the angles at the corner points marked with those letter, and (a,b,c) will be the lengths of the sides facing the corners (A,B,C).
To the diagram drawn earlier to illustrate the center of mass of the Earth-Moon system, we add a spacecraft at some point C, with distances b from the Earth, a from the Moon and R from the center of mass D. As in the derivation of the law of sines, we name (A,B,C) the angles at the corner points marked with those letter, and (a,b,c) will be the lengths of the sides facing the corners (A,B,C). We furthermore label as (α,β) the two parts into which R divides the angle C. Check all these out before continuing. The question to be answered is: Under what conditions does the satellite at C maintain a fixed position relative to the Earth and Moon? The calculation is best handled in the frame rotating with the Moon. In that frame, if a satellite at point C is in equilibrium, it will always keep the same distance from the Moon and from Earth. The center of rotation is the point D--even the Earth rotates around it--and if the spacecraft at C is in equilibrium, all three bodies have the same orbital period T. If C is motionless in the rotating frame, there exists no Coriolis force (it only acts on objects moving in that frame), but the spacecraft will sense a centrifugal force, as will the Moon and the Earth.
Let us collect equations--the ones which the distances and angles must obey.
(1) Note first that the radius of rotation R of the spacecraft will Denoting the rotational velocity of the Moon by V and that of the spacecraft by v, since distance = velocity x time
The two expressions equal to 2π/ T must also be equal to each other, hence (1) v/R = (V/c)(1 + m/M) This merely expresses the well-known observation that if two objects share a rotation, the one more distant from the axis rotates faster, and their velocities are proportional to their distances from the axis.
(2) The centrifugal force on the Moon is
(2) GM/c = V2 (1 + m/M)
(3) Let m' be the mass of the spacecraft. The centrifugal force on it is
Now by Newton's theory of gravitation
Inserting these in the upper equation and dividing both sides by m' gives the 3rd equation: (3) v2/R = (Gm/a2) cosβ ;+ (GM/b2) cosα
(4) Finally, the forces pulling the spacecraft in directions perpendicular to R must cancel. Otherwise, the spacecraft would be pulled by the stronger of the two and would not stay at C, that is, would no longer be in equilibrium. That requires
(4) (m/a2) sinβ = (M/b2) sinα
Collecting all equations once more:
The quantities appearing here are of 3 types.
We already carried out an elimination earlier. We had two equations which involved the orbital period T, each was used to express 2π/T, and by setting those two expressions equal to each other, we obtained a single expression which did not contain T (we always "give up one equation" in an elimination process--start with two, end with one). The plan then is as follows. We will eliminate V between (1) and (2), leaving an equation involving only v. Then we will eliminate v between it and (3), winding up with an equation not involving velocities--plus (4), which also contains neither v nor V. From (1), squaring both sides
Multiply both sides by c2 and divide them by (1 + m/M)
But by (2) (5) v2 (c2/R2) /[1 + m/M] = GM/c and V has just been eliminated. Now multiply both sides by (1 + m/M), divide them by c2 and multiply them by R
Therefore (moving a factor of 1/c to R)
Dividing everything by GM gives one of the equations we are left with, while the other one is (4): (6) (1/c2) (R/c) (1 + m/M) = (1/a2)(m/M) cosβ+ (1/b2) cos α (4) (m/a2) sinβ = (M/b2) sinα Rather complicated! However, we have already peeked at the answer and suspect that good things might happen if the triangle ABC is equilateral--if all its angles are 60° and all its side are equal to the same length, which we will denote r:
In that case, if the above equations are multiplied by r2, the factors (1/a2), (1/b2) and (1/c2) all disappear, leaving (7) (R/c)(1 + m/M) = (m/M)cosβ + cosα (8) m sinβ= M sinα From here m/M = sinα/sinβ Substitute this on the right side of (7)
sin β ;(R/c)(1 + m/M) = sinαcosβ+ cosαsinβ = sin(α + β) = sin C = sin B
The last equality comes because all three angles (A,B,C) are equal. That however is no more than the law of sines in the triangle CDB and is therefore obviously fulfilled. Working backwards from here, one can now show that all preceding equations, down to (1) through (4), are satisfied if ABC is equilateral. Therefore C is a point of equilibrium in the rotating frame. If we had not assumed the triangle ABC to be equilateral and the distances (a,b,c) to be equal, we would have obtained a relation different from the law of sines, one which did not hold, and therefore all equations required for equilibrium at point C could not be satisfied.
As already noted, because L4 and L5 are stable points of equilibrium, they have been proposed for sites of large self-contained "space colonies", an idea developed and advocated by the late Gerald O'Neill. In 1978 Bill Higgins and Barry Gehm even wrote for would-be colonists "The L5 Song " to the tune of "Home on the Range. " Here is its beginning:
Home on Lagrange
Where the gravitons focus Where the three-body problem is solved Where the microwaves play Down at 3 degrees K And the cold virus never evolved
CHORUS:
Exploring Further:About space colonies at Lagrangian points:
About the L4 and L5 points and about asteroids locked into the neighborhoods of L4 and L5 of the Sun-Jupiter system: "When Trojans and Greeks Collide" by I. Vorobyov, Quantum, September-October 1999, p. 16-19. That article contains an alternative proof of the equilibrium of motion at L4 and L5, more general (no limitation on the masses) but using a rotating frame of reference and two-dimensional vectors. The calculation can be found in section (34-c) of this web site. |
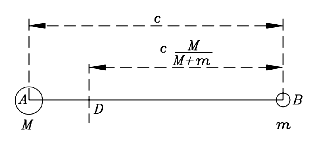 As shown in
As shown in 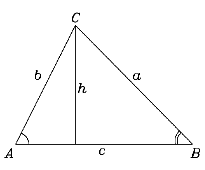 Let us prove it for the angles A and B, by drawing from the third corner C a line perpendicular to the opposite side of the triangle. Let h be the length of that line. Then
Let us prove it for the angles A and B, by drawing from the third corner C a line perpendicular to the opposite side of the triangle. Let h be the length of that line. Then