|
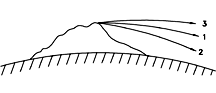
This is the velocity required by the satellite to stay in its orbit ("1" in the drawing). Any slower and it loses altitude and hits the Earth ("2"), any faster and it rises to greater distance ("3"). For comparison, a jetliner flies at about 250 m/sec, a rifle bullet at about 600 m/sec. We again need a notation for square root. Since the HTML language does not provide one, we use the notation SQRT found in some computer languages. The square root of 2, for instance, can be written SQRT(2) = 1. 41412. . . If the speed V of our satellite is only moderately greater than Vo curve "3" will be part of a Keplerian ellipse and will ultimately turn back towards Earth. If however V is greater than 1. 4142. . .times Vo the satellite has attained escape velocity and will never come back: this comes to about 11.2 km/sec. The value of 11.2 km/s was already derived in the section on Kepler's 2nd law, where the expression for the energy of Keplerian motion was given (without proof) as where for a satellite orbiting Earth at distance of one Earth radius RE, the constant k equals k=gRE2. The energy is negative for any spacecraft captured by Earth's gravity, positive for any not held captive, and zero for one just escaping. Let V1 be the velocity of such a spacecraft, located at distance RE but with zero energy, i.e. E=0. Then Kepler's Third Law for Earth SatellitesThe velocity for a circular Earth orbit at any other distance r is similarly calculated, but one must take into account that the force of gravity is weaker at greater distances, by a factor (RE/r)2. We then get V2/r = g (RE r)2 = g RE2/r2 Let T be the orbital period, in seconds. Then (as noted earlier), the distance 2 πr covered in one orbit equals VT |
| VT | = 2 π r |
| V | = 2 π r/T |
| V2 | = 4 π2r2/T2 |
| V2/r | = 4 π2 r/T2 |
|
and by the earlier equality 4 π2r/T2 = g RE2/r2 Get rid of fractions by multiplying both sides by r2T2 4 π2r3 = g RE2 T2 To better see what we have, divide both sides by g RE2, isolating T2: T2 = (4 π2/g RE2) r3 What's inside the brackets is just a number. The rest tells a simple message--T2 is proportional to r3, the orbital period squared is proportional to the distance cubes. This is Kepler's 3rd law, for the special case of circular orbits around Earth. If you are not yet tired of the calculation, you may click here for turning the above into a practical formula. Questions from Users: Spaceflight without escape velocity? *** Does the solar wind have escape velocity |
Deriving a practical formula from Kepler's 3rd law.
Next Regular Stop: Frames of Reference: The Basics
Timeline Glossary Back to the Master List
Author and Curator: Dr. David P. Stern
Mail to Dr.Stern: stargaze("at" symbol)phy6.org .
Last updated: 9-22-2004
Reformatted 24 March 2006